Flight profile

We’ll begin by looking at the flight as a whole, and the parameters that determine the height and speed at each point along the route.

The trajectory

Figure 1

A flight can be divided into three phases: climb, cruise, and descent (figure 1). During the initial climb, the engines have to work hard and consume fuel at a greater rate. One can save fuel by climbing slowly, but this delays the point at which the aircraft reaches cruise height, where the air resistance is less. There is a specific mathematical technique for optimising the climb phase in conjunction with the subsequent cruise phase; it is called the energy state approach [9]. We won’t go into the details here, but concentrate on the ‘cruise’ phase alone, which is the most important phase on a long flight.

Unless it’s a short journey, a large aircraft will spend much of the time cruising on ‘auto-pilot’ or what is known more formally as automatic flight control, a system which the pilot will program in advance to maintain a given course at a given speed and altitude. Smaller aircraft are controlled manually. Either way, one might imagine that in technical terms, the analysis of cruising flight is a simple matter. However, there is a complication. It arises from the fact that aircraft must carry fuel. Fuel is heavy, and its weight diminishes during the journey. The problem isn’t limited to aircraft: birds that migrate over long stretches of ocean or desert start out with a large quantity of body fat – the ‘fuel’ needed to keep them flying – that amounts to roughly a third of their total weight [1]. Aircraft are not very different. On a long flight, almost half the weight of a modern airliner may be taken up by fuel. Its weight decreases gradually with distance, and when we analyse the flight profile, ideally we should take this into account because it changes the aircraft’s aerodynamic behaviour. We’ll return to this aspect later, but for the moment, we’ll assume the flight is a short one that takes place at a steady speed \(V\), so \(V\) is constant, and picture the aircraft as carrying a fixed fuel load, so the total weight \(W\) is constant. Note that \(W\) has units of force, being equal to the aircraft mass times \(g\). We’ll also assume a straight and level course, so that the lift force \(L\) needed to support the aircraft is equal to \(W\).

Flight parameters

When flying outside the regions covered by Air Traffic Control, the pilot can plan the flight trajectory to suit the terrain and the weather conditions en route. Let’s begin with the question of altitude. For obvious reasons, the aircraft must maintain a safe height above the ground so that if something goes wrong such as an engine failure or a temporary loss of control, the pilot has time to recover the situation and if necessary, find somewhere to land. In fact, on a long-distance flight, a jet aircraft will spend much of the time cruising far above the earth’s surface where the air is cold and thin. There are three reasons for this:

1. Flying above the clouds means less turbulence and a smoother ride.
2. At an altitude of 10 000 metres, the air is thinner and offers less resistance.
3. The air is coldest at this altitude, at about -50\({^\circ}\)C, which makes a jet engine thermally more efficient [6].

It follows that for a jet aircraft, flying at a high altitude is more economic, because the aircraft can travel further or faster on a given quantity of fuel.

So what about the speed? When flying fast, the rate of fuel consumption per kilometre increases, and the saving in journey time may be small in relation to the extra cost. Also, the formation of local shock waves may cause buffeting so the vehicle becomes increasingly difficult to control. Surprisingly perhaps, the fuel consumption rises at the lower end of the speed range too. To fly slowly, the aircraft must be pitched at a high angle of attack so the wings generate sufficient lift to carry its weight. This creates extra drag, with the result that the engines must work hard and again, burn more fuel. Also, flying slowly increases the risk of a stall. Usually, therefore, the pilot avoids flying at a speed near either end of the range, and it’s useful to know where the limits might lie.

The speed range

At one end of the range is the minimum speed – the speed at which the aircraft stalls - while at the other is the maximum speed it can achieve at full throttle. To fly at the stalling speed is risky. The pilot can do this deliberately by pitching the nose up until the aircraft is only just able to keep going at its existing height. For any particular machine, the stalling speed is determined by the maximum value of the coefficient of lift \(C_{L} {}_{max}\). In turn, the value of \(C_{L} {}_{max}\) depends on the angle of attack and the aerodynamic behaviour of the wings, and can only be determined by experiment. Assuming the value is known, we can estimate the stall speed \(V_{S}\) from the empirical lift formula

where \(\rho\) is the air density and \(A\) the plan area of the wings. By substituting \(C_{L} {}_{max}\) for \(C_{L}\) and the aircraft weight \(W\) for \(L\), and then re-arranging the equation, we get

Note this applies only to straight and level flight: the stall speed increases during a turn.

At the other end of the range, the maximum speed \(V_{max}\) depends not only on the aerodynamics, but on the engine power as well. Assuming subsonic flight in which compressibility effects can be ignored, we can determine its value from the drag polar. The drag polar is a key formula in aerodynamics that we met earlier in Section A1716. It relates the lift coefficient \(C_{L}\) and the drag coefficient \(C_{D}\):

We treat the other three quantities in equation 3 as constant for a given aircraft: \(C_{D,0}\) is the parasitic drag coefficient at zero angle of attack, \(E\) (in our notation) is the Oswald Efficiency Factor, and AR is the wing aspect ratio. We can now estimate the aircraft’s maximum speed, and we start by converting equation 3 into a relationship between the lift \(L\) and drag \(D\), by making two substitutions. First, we substitute for \(C_{L}\) using the empirical lift formula in equation 1, then we substitute for \(C_{D}\) using the equivalent formula for drag \(D={\rm \; }\tfrac{1}{2}\rho V^{2} AC_{D}\). Then we assume level flight, so the drag \(D\) equals the available engine thrust \(T\), and the lift equals the aircraft weight \(W\). Finally, we assume the speed is maximised when the engines are delivering maximum thrust \(T_{max}\). The result can be expressed as a quadratic equation that can be solved to yield an expression for \(V_{max}\). The details are set out in [4]. We won’t repeat them here but give the result in a slightly different form:

It spells out many of the requirements for a high-speed aircraft. The first and most obvious requirement is to maximise \(T_{max} /W\), the ratio of engine thrust relative to the aircraft weight. Second, we need to minimise the zero-lift drag coefficient \(C_{D,0}\). Third, the aircraft should fly as high as possible where the air density \(\rho\) is low. Finally, the ratio \(W/A\) should be large. This ratio has a special place in aeronautical engineering: it is known as the wing loading, and its value has risen over the decades with each new generation of aircraft. The reason is not hard to find. For an aircraft of any given weight, the higher the wing loading, the smaller the wing area, and a small wing generates less friction drag. The wing loading of a Boeing 747 is roughly 100 times that of the original Wright Flyer of 1903 [8].

However, the formula is not reliable for aircraft that cruise at higher speeds bordering the transonic range. As described earlier in Section A1615, within this regime, local shock waves form over the wings and cause buffeting. Here, drag divergence sets in. For a commercial aircraft, it is the drag divergence that effectively limits the maximum speed.

Altitude

Moreover, since the speed of sound falls with increasing altitude, the speed at which drag divergence and buffeting begins must fall too, and with it, the upper limit of the safe range of flying speeds. At the same time, since the air density falls we see from equation 2 that the stalling speed rises. The combination of the rising lower limit and the falling upper limit narrows the range of feasible cruising speeds, so that as the altitude increases, eventually the aircraft reaches an impasse: any change in speed results in loss of lift, a situation known among pilots as ‘coffin corner’ [7].

Partly for this reason, all aircraft have a designated service ceiling. For practical purposes it’s derived from flight tests centred on the aircraft’s rate of climb. Starting from ground level, modern transport aircraft can climb at a rate of 3000 – 5000 feet/minute, but the climb rate falls with increasing height. So we designate the absolute ceiling as the altitude at which the aircraft cannot climb any further because its rate of climb is zero. This is not a safe flight condition, and the service ceiling is taken as the altitude for which the rate of climb is 100 feet/minute [3].

Criteria for efficient flight

Commercial aircraft are expensive to run. On any given journey, the pilot will try to ensure the plane is being used efficiently. ‘Efficiency’ is a broad term that may involve several different goals, such as minimising fuel consumption, maximising journey speed, and so on. Different goals call for different flying strategies, and in what follows, we’ll consider what the pilot must do to achieve them.

The core relationship

At the heart of the efficiency question lies the relationship between lift \(L\) and drag \(D\). In fact, the ratio of lift to drag is itself a useful measure of efficiency in a general sense: the greater the ratio, the less the drag, and the less the wasted energy. For any given aircraft, the ratio \(L/D\) varies during each flight, but what we’re really interested in is sustained flight at the maximum value \(\left(L/D\right)_{max}\). For many aircraft, the maximum lies in the region of 10:1 (exceptionally, for the Boeing 747, it is 20:1 [5]. For transonic and supersonic aircraft, the value is typically much less.

For some purposes, the relationship between the lift \(L\) and the drag \(D\) can conveniently be expressed in terms of the relationship between their respective drag coefficients \(C_{L}\) and \(C_{D}\). This relationship is embodied in the drag polar as set out earlier in equation 3. In Section A1716, the curve was plotted in Figure 11 with the lift coefficient as the ordinate. Here, we show the same curve turned through a right-angle with the drag coefficient as the ordinate (figure 2). As we’ll now see, one can use this relationship to establish the speed at which the aircraft must fly to meet specific criteria.

Figure 2

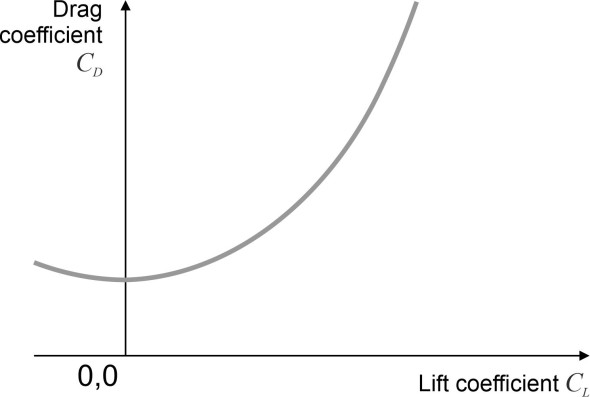
Minimum drag

A good place to start is the speed at which the drag takes on the minimum possible value, which we’ll denote the by \(V_{min{\rm \; }drag}\). Looking at figure 2, it would seem that the minimum coefficient of drag arises where the curve crosses the \(C_{D}\) axis, at \(C_{L} ={\rm \; }0\). This cannot be the solution we are looking for, because it implies zero lift, whereas in reality, the lift coefficient must have a finite positive value if the wings are to support the weight of the aircraft. In other words, we should seek the minimum drag coefficient subject to the constraint that \(L=W\).

This is the purpose of the Appendix at the end of this Section. Starting from the drag polar in equation 3 above, we show that

Flying at this speed is aerodynamically efficient, but it’s not necessarily the speed that the pilot will choose, for two reasons. First, the main concern may not be the drag as such, but the cost of running the aircraft including the costs to users: for example, if the passengers place a high value on their travel time, they might prefer to go faster. Second, there is the question of stability. Figure 3 shows diagrammatically how the drag varies with speed.

Figure 3

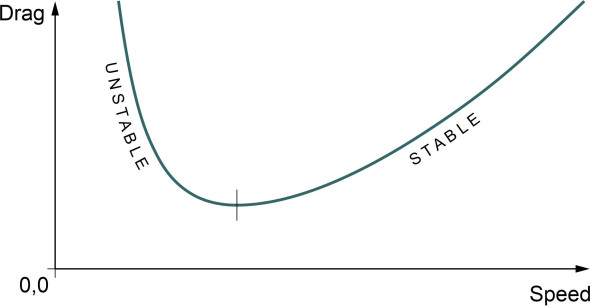
The curve has two arms, and the speed condition for minimum drag is represented by the point where they meet at the bottom. Imagine what happens when the pilot chooses a target speed that lies on the left-hand arm, indicated on the curve by the letter ‘A’, and suppose there is a gust of wind from behind that momentarily reduces the speed of the air flowing over the wings. Because of the reduced air speed, the point A moves to the left, rises a little way up the curve, and the drag increases. Hence the aircraft will continue to lose speed and the pilot must take corrective action to prevent the drag from rising to the point where the aircraft stalls. By contrast, if the aircraft is flying at a target speed indicated by the letter ‘B’ on the right-hand arm of the curve, the opposite occurs. The wind gust still causes the effective air speed to fall, but as it falls, the drag falls too. Hence the aircraft tends to speed up of its own accord. Thus we see that flying faster than the speed corresponding to minimum drag reduces the burden on the pilot and makes the flight safer for all concerned.

Nevertheless, the speed corresponding to minimum drag remains a key reference point for the aircraft designer. In the Appendix we also derive an expression for the minimum drag itself, thus:

Minimum power

When an aircraft is flying horizontally at constant speed, the engines must supply a thrust \(T\) that is equal and opposite to the drag. We have discovered that by flying at a particular speed, the pilot can minimise the thrust needed to keep the aircraft going. But there is another way to view the problem. Over any given distance, the energy consumed in overcoming the drag \(D\) is equal to \(D\) times the distance travelled, and if the aircraft is travelling at speed \(V\), the rate of energy consumption per unit time is \(DV\). By definition, this is the power \(P\) drawn from the engines. This raises an interesting possibility for the designer. Powerful engines are heavy and consume more fuel than less powerful ones. Why not fly at the speed \(V_{min{\rm \; }power}\) that minimises the power required?

In the Appendix attached to this Section, we derive an expression for \(V_{min{\rm \; }power}\) thus:

It is not the same as the speed required for minimum drag. Compared with equation 5, the right-hand side of equation 7 contains an additional factor \(3{}^{-1/4}\), so it works out at about 24% less. Oddly, although the aircraft is flying with less power, it is creating more drag. Notice also that the solution lies on the unstable arm of the curve shown in figure 3, which suggests that flying at this speed might increase the pilot’s workload.

Cruising

Having looked at the conditions for minimum drag and minimum power, we can now turn to two other criteria - range and endurance – that emerge from the results obtained so far. Once it has taken off, the aircraft is almost completely isolated from the everyday world, in the sense that its progress depends on how much fuel it is carrying and the rate at which it is consumed before the aircraft must land and re-fuel. The range is the distance the aircraft can travel, while the endurance is the time it can remain aloft.

Range and endurance

Range is important for a commercial airline: passengers prefer to travel non-stop if possible, and it is in the interests of the operator to avoid intermediate stops that entail extra costs such as airport landing fees together with the additional fuel consumed during each take-off and climb. Endurance is important too, mainly for certain types of flight in which the aircraft has no particular destination, but is required to maintain a presence in the sky. This is sometimes the case with military aircraft on patrol, and aircraft carrying out various forms of research into atmospheric conditions for example.

In what follows, we’ll work out the speed at which an aircraft should travel to maximise its range, and the speed at which it should travel to maximise endurance. On any flight, the condition for maximum range is that the engines consume the minimum weight of fuel per unit distance. The condition for maximum endurance is that the engines consume the minimum weight of fuel per unit time. These are two different conditions, and the ‘optimum’ speeds are different. And as mentioned earlier, there is a complication: on a long journey, the total weight \(W\) of the aircraft falls as it consumes fuel, and hence the optimum speeds change during the flight. Therefore, we break the journey down into short segments and look at a typical segment, treating it as if the weight were constant.

Engine power

By way of preparation, it will help to consider the notion of engine ‘power’ in a little more depth. In steady flight at constant speed and altitude, an engine produces thrust that pushes the vehicle forward, and the thrust must be equal and opposite to the aerodynamic drag, fuselage and tail. But piston engines and jet engines react differently as the speed rises. The thrust \(T\) available from a piston engine and propeller is greatest at standstill, and it falls with increasing speed [2]. This is because the faster the oncoming flow meets the propeller, the faster the blades must rotate round the propeller shaft to maintain a positive angle of attack and the greater the friction drag, a matter that we touched on earlier in Section F1513. Eventually, the speed of the propeller tips approaches the speed of sound, which places an upper limit on the thrust they can produce. However, the power output \(VT\) is roughly constant throughout a large part of the speed range. By comparison, the thrust \(T\) available from a turbojet is roughly constant with increasing speed \(V\). It doesn’t fall away as the speed rises, because when an aircraft moves fast, the air that a turbojet needs for combustion is rammed into the air intake at increasingly high pressure. And because the thrust remains unchanged, the power output \(VT\)rises with increasing speed. In this sense, jet engines are most economical when flying fast.

The result is that in practice, engineers define the fuel consumption of the two different types of aircraft in two different ways. For a propeller-driven aircraft, it is taken as the rate of fuel burn per unit time per unit power output. By contrast, the fuel consumption for a turbojet is typically defined as the fuel burned per unit time per unit thrust, and in fact, the power output increases linearly with speed. We have only sketched the outline of what is a broad subject here, and readers seeking more information might turn to [10].

Propeller-driven aircraft

Let’s start with a propeller-driven aircraft, and consider a typical journey segment during which the aircraft travels a distance \(\delta x\) in time \(\delta t\). The fuel consumption \(c_{P}\) is defined as the weight of fuel consumed per unit power per unit time, so that during our time interval \(\delta t\), when the engine power output is \(P\), we have:

To maximise endurance, we minimise the fuel consumed per unit time. Over the time interval \(\delta t\), this is the weight of fuel consumed divided by \(\delta t\). From equation 8, this is equal to \(Pc_{P}\), and since \(c_{P}\) is constant, minimising the fuel consumption amounts to minimising the power \(P\). We have already derived an expression for the speed \(V_{min{\rm \; }power}\) at which the power is minimised, which is given by equation 8 above. The curve in figure 4 shows the drag \(D\) plotted against velocity \(V\), with the condition for maximum endurance marked at point ‘A’.

Figure 4

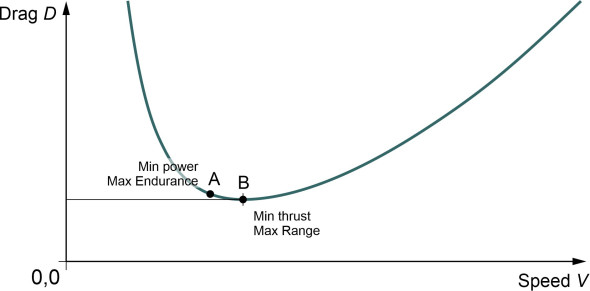
Now for the maximum range. In this case, we want to minimise the fuel consumed per unit distance, which in any given interval is the weight of fuel divided by \(P\delta x\). The time \(\delta t\) taken to travel a distance \(\delta x\) equals \(\delta x/V\), and if we substitute \(\delta x/V\) for \(\delta t\) in equation 8 and rearrange, we get

For our journey segment, the fuel consumed per unit distance is the weight of fuel divided by \(\delta x\), and from equation 9, we see this is equal to \(Tc_{P}\). So to obtain maximum range, we must minimise the thrust \(T\). In level flight this is the same as the condition for minimum drag, which means travelling at a speed \(V_{min{\rm \; }drag}\) as specified earlier in equation 5. This flight condition marked as point ‘B’ at the lowest point on the curve in figure 4.

Also, we see from equation 5 that \(V_{min{\rm \; }drag}\) is proportional to the square root of the aircraft weight \(W\), which falls as fuel is consumed during the flight, so the speed itself must fall from one segment to the next. It follows that, although we know how fast the aircraft must fly to maximise its range during each segment of the journey, we don’t yet have a formula for the maximum range itself. The same applies to the endurance. In principle, both can be calculated using numerical methods, but the calculations are laborious. For propeller-driven aircraft, there is a long-standing formula known as the Breguet formula that gives an approximate estimate of the maximum range; it was used extensively during early decades of aircraft flight. Today, computer-based numerical methods can provide more accurate results.

Jet aircraft

Now we turn to aircraft powered by turbojet engines. The fuel consumption \(c_{T}\), which we assume is approximately constant, is defined as the weight of fuel burned per unit time per unit thrust so that for our journey segment:

To maximise endurance, we minimise the fuel consumed per unit time, which we deduce from equation 10 is equal to \(Tc_{T}\). Since \(c_{T}\) is a constant, this amounts to minimising the thrust \(T\), which is equivalent to minimising the drag \(D\). This is the same as the condition for maximising the range for a propeller-driven aircraft, and figure 5 shows it marked at the lowest point C of the curve of drag against velocity.

Figure 5

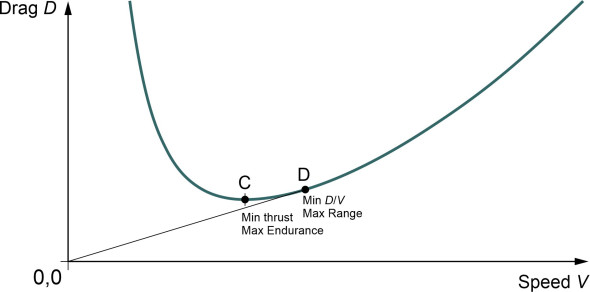
Now for the maximum range. In this case, we need to minimise the fuel consumed per unit distance. During our journey segment, the aircraft will travel a distance \(\delta x=V\delta t\), so we can substitute \(\delta x/V\) for \(\delta t\) in equation 10 and rearrange it to get

Therefore, to minimise fuel consumed per unit distance, we must minimise \(c_{T} T/V\). Since \(T=D\) and \(c_{T}\) is constant, this is equivalent to minimising \(D/V\). Now the ratio \(D/V\) is the slope of a line drawn through the origin of the graph in figure 5, and the line with minimum slope is the tangent to the curve at D, hence the condition for maximum range is the point D.

What we have learned from this rather extended analysis is that there are significant differences in the speeds that optimise the aircraft’s performance depending (a) on the type of engine and (b) whether we seek maximum range or maximum endurance. They are interesting from a theoretical point of view and provide benchmarks for the designer, but since they all lie close to the lowest point on the curve of drag against velocity in figure 4 and figure 5, small variations on either side of the optimum values don’t greatly affect the outcome for any given segment of the flight. The most important conclusion is that the aircraft should fly close to the speed for minimum drag, and therefore to be competitive, \(V_{min{\rm \; }drag}\) should be as high as possible. Equation 5 tells us a lot about the conditions under which this can be achieved. The first term on the right-hand side suggests that to fly fast, the air density \(\rho\) should be low, so a jet aircraft will perform best when flying high. In addition, the wing loading \(W/A\) should be high. Given that these conditions are met, the main challenge for the pilot is maintain a speed close to the value for minimum drag – preferably, for safety reasons a little above - and when carrying a heavy fuel load on a long flight, to reduce the flight speed in an appropriate fashion as the weight of the aircraft falls.

Comment

In this Section, we’ve looked at some of the factors that should be taken into consideration when determining how high and how fast an aircraft should fly. One of the most important factors is fuel economy, not only because fuel is expensive, but because the more fuel the aircraft carries, the more fuel it will burn carrying it, and the smaller the payload of passengers and cargo. We’ve observed that the cruising speed that minimises fuel consumption is different for turbojet aircraft and propeller-driven aircraft. For turbojets, the most economical speed corresponds to minimum drag. For propeller-driven aircraft, it corresponds to minimum power. But these are theoretical benchmarks. In practice, the pilot – especially if flying a propeller-driven machine - will want to fly a little faster, within the stable region of the drag curve. And on the question of altitude, for jet aircraft there are conflicting influences at work. First, jet engines are more efficient at high altitudes where the air is cold, so up to a point, the thrust is not greatly affected by the thin atmosphere. Jet aircraft perform best when flying high. On the other hand, for a subsonic aircraft the range of safe speeds shrinks with increasing altitude to a point that leaves little margin for the pilot cope with unexpected variations in wind speed or air temperature. There is a limit to the height at which the aircraft can safely fly. Occasionally, it will meet a thunderstorm that is too widely spread to fly around, and too tall to fly over. The only option is to turn back.

Appendix: Critical speeds

Here we shall develop formulae for speeds at which the aircraft must travel firstly to minimise the drag, and secondly, to minimise the power extracted from the engines. As before, we begin with the drag polar as set out earlier in equation 3, which is repeated below:

Next we turn to the standard empirical drag formula

and re-arrange it to yield an explicit expression for \(C_{D}\) that we substitute for the left-hand side of equation 12. The result is

Now, the empirical formula for lift is:

and since in straight and level flight \(L=W\) this can be written

so that in equation 14, we can replace the expression \(\tfrac{1}{2}\rho V^{2} A\) by \(W/C_{L}\) to get

The only variable on the right-hand side is \(C_{L}\). We can find the minimum value of \(D\) by differentiating the right-hand side with respect to \(C_{L}\) and equating the result to zero thus:

from which we deduce that the coefficient of lift that corresponds to minimum drag, which we’ll denote by \(C_{L} {}_{min{\rm \; }drag}\), is given by

We can substitute this for \(C_{L}\) in equation 16 to yield

from which it follows that the speed \(V_{min{\rm \; }drag}\) at which the drag is minimised is given by:

Since in level flight at constant speed, the thrust from the engines exactly counterbalances the aerodynamic drag acting on the aircraft, this is also the condition for minimum thrust. It represents the most efficient configuration for a flying machine, and although aircraft don’t necessarily fly at this speed very often, it forms a central reference point for aircraft design.

Our second derivation concerns the conditions for minimum power, which are different from the ones for minimum thrust. For level flight at constant speed, the power \(P\) represents the rate of energy output required per unit time, so that

Substituting for \(D\) from equation 14 leads to:

while re-arranging equation 16 gives:

Substituting for \(V\) in equation 23 and re-arranging leads to:

We can now differentiate \(P\) with respect to \(C_{L}\) and equate the result to zero. After tidying up, we get:

from which it emerges that the coefficient of lift \(C_{L} {}_{min{\rm \; }power}\) corresponding to minimum power is

Finally, after substituting the above for \(C_{L}\) in equation 16 we deduce that the speed \(V_{min{\rm \; }power}\) at which the required power output is minimised is

Comparing this with equation 21, the only difference is the factor \(3{}^{-1/4}\). Hence for minimum power, \(V_{min{\rm \; }power}\) works out at roughly \(0.76\; V_{min{\rm \; }drag}\), and the aircraft must fly more slowly.